图形变换

Model Transforms

基础定义

• 图形在坐标系中的变换如果可以用一个矩阵表示，即$\left(\begin{array}{c}x\\ y\end{array}\right)\times M=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)$ 则说这个变换为线性变换。
• 满足线性变换定义的变换包括：缩放，切变，旋转。
• 平移不属于线性变换，为了兼容平移，需要引入齐次坐标。
• 由于表示点或向量使用的矩阵为竖式，所以所有的变换矩阵需要左乘，即$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=M_n\times \cdots \times M_2\times M_1\times \left(\begin{array}{c}x\\ y\end{array}\right)$，为了免除坐标的多次运算，可以将左侧所有的变换矩阵使用结合律先运算，即$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=(M_n\times \cdots \times M_2\times M_1)\times \left(\begin{array}{c}x\\ y\end{array}\right)$
• 引入了齐次坐标后，需要对点与向量进行区分，点需要添加坐标1，向量需要添加坐标0。即 $point=\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$ $vector=\left(\begin{array}{c}x\\ y\\ 0\end{array}\right)$
• 点的齐次坐标不为1时，即$point=\left(\begin{array}{c}x\\ y\\ w\end{array}\right)$，则该点表示的实际坐标为$point=\left(\begin{array}{c}x/w\\ y/w\\ 1\end{array}\right)$
• 如果需要进行线性变换后平移变换，需要先线性变换，再平移变换，交换顺序后得到的结果大概率不一致。
• 一个变换矩阵的逆矩阵可以将点或向量移回原处，即$p=M\times M^{-1}\times p$，所以对于不在原点的图像或向量，可以先将其移回原点，线性变换后再移回原处，即设平移矩阵为$T(c)$，则可以$T(c)\cdot T(\alpha )\cdot T(-c)$

线性变换的矩阵

2D变换

缩放（Scale）

• $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}{S}_x& 0\\ 0& S_y\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

切变（Shear）

• $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& cos{\theta }_x\\ sin{\theta }_y& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

旋转（Rotate）

• $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$

平移（Transform）

• 使用线性变换无法得出平移的矩阵$M$，只能使用矩阵加法计算得出。

$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}{t}_x\\ t_y\end{array}\right)$

为了使平移变换可以容纳进线性变换，需要添加齐次坐标。

$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right)=\left(\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$

3D变换

缩放（Scale）

• 类似2D下的缩放变换 $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right)=\left(\begin{array}{cccc}{S}_x& 0& 0& 0\\ 0& S_y& 0& 0\\ 0& 0& S_z& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)$

切变（Shear）

• 暂无

旋转（Rotate）

• 根据不同的旋转轴，需要使用不同的旋转矩阵 三个旋转矩阵可以通过右手直角坐标系叉乘得到

$R_x(\alpha )=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\alpha & -sin\alpha & 0\\ 0& sin\alpha & cos\alpha & 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)$

$R_y(\alpha )=\left(\begin{array}{cccc}cos\alpha & 0& sin\alpha & 0\\ 0& 1& 0& 0\\ -sin\alpha & 0& cos\alpha & 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)$

$R_z(\alpha )=\left(\begin{array}{cccc}cos\alpha & -sin\alpha & 0& 0\\ sin\alpha & cos\alpha & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)$

• 对任意一个旋转可以分解成三个简单的绕轴旋转，即：$R_{xyz}(\alpha ,\beta ,\gamma )=R_x(\alpha )R_y(\beta )R_z(\gamma )$ 在这个公式中，$\alpha$，$\beta$， $\gamma$这三个角被称为欧拉角（Euler angles）
• 罗德里格旋转公式（Rodrigues's Rotation Formula）

罗德里格旋转公式是计算三维空间中，一个向量绕旋转轴旋转给定角度以后得到的新向量的计算公式。这个公式使用原向量，旋转轴及它们叉积作为标架表示出旋转以后的向量。可以改写为矩阵形式，被广泛应用于空间解析几何和计算机图形学领域，成为刚体运动的基本计算公式。

$$R(n,\alpha )=cos(\alpha )\mathbf{I}+(1-cos(\alpha ))n{n}^T+sin(\alpha )\left(\begin{array}{ccc}0& -n_z& n_y\\ n_z& 0& -n_x\\ -ny& n_x& 0\end{array}\right)$$

平移（Transform）

• 类似2D下的平移变换 $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right)=\left(\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)$

• View/Camera Transformation

基础定义

• model transformation 模型变换
• view transformation 视角变换
• projection transformation 投影变换 以上三种简称MVP变换

定义一个相机

三元素

• 位置（Position） $\overrightarrow{e}$
• 视角方向 （look-at/gaze direction） $\hat{g}$
• 相机的上方向 （up direction） $\hat{t}$

定义一个相机

• 定义一个相机时，通常将相机放在原点上，向$-z$方向看，以$y$轴为上方向 对于任意一个相机，满足以上条件需要进行以下几步操作 对于一个相机$M_{view}=R_{view}{T}_{view}$
• 将相机移动到原点

$$T_{view}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right]$$

• 将视角$\hat{g}$旋转到$-z$方向
• 将上方向$\hat{t}$旋转到$y$方向
• 将视角与上方向的叉乘$(\hat{g}\times \hat{t})$旋转到$x$方向 考虑如何得出$R_{view}$很困难，所以可以先考虑出如何从结果反推出矩阵，即

$$R_{view}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

由此可得出：

$$R_{view}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

• Projection Transformation

基础定义

• 投影是3d向2d的渲染，主要分为正交投影（Orthographic projection）以及透视投影（Perspective projection）
• 正交投影一般用于工程视图，不会出现近大远小效应
• 透视投影一般是现实中的相机，会出现近大远小效应

正交投影

相机设置

方法一

• 将相机放在原点上，看向$-z$方向，上方向为$Y$
• 去掉$Z$轴，将所有的内容全部放在x与y组成的平面中
• 将结果缩放到一个$[-1,1{]}^2$的矩形中

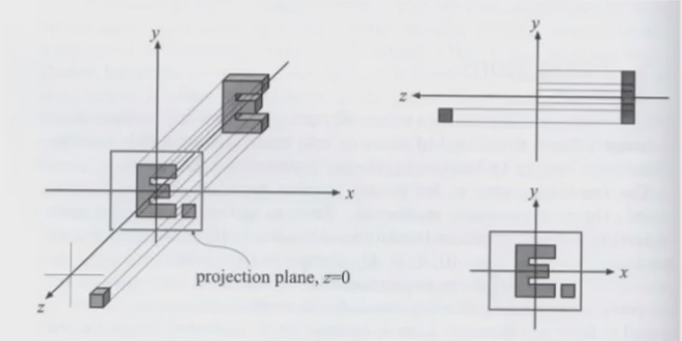
方法2

• 定义好模型的$[l,r]\times [b,t]\times [f,n]$
• 将模型移动到原点上
• 将模型缩放到一个标准正方体（canonical cube）中
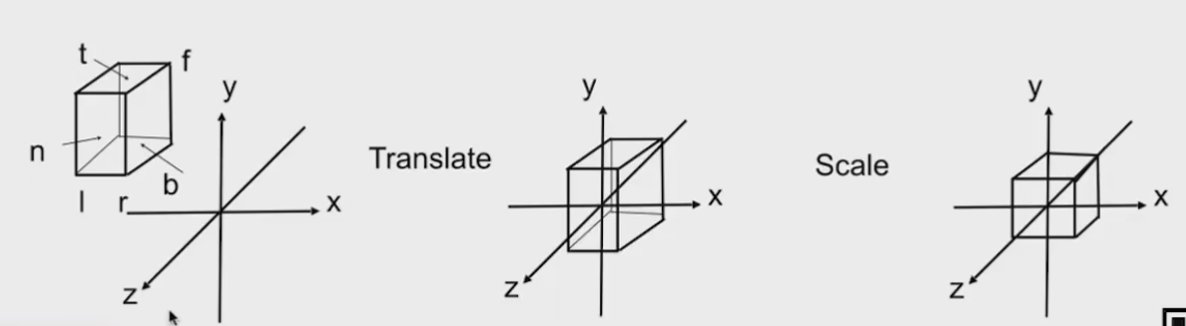
• 数学上的表示

$$M_{ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$$

透视投影

基础定义

• 透视投影需要从一个点，延申出一个四棱锥，这个四棱锥就是相机。
• 将远平面挤压成一个与近平面一样大小的四边形，然后做一次正交投影，即为透视投影，即需要得出$M_{persp\to ortho}$
• 挤压远平面时需要规定几点：

1. 近平面永远不会变化
2. 远平面在挤压后，z值不会变化
3. 远平面的中点在挤压后，仍为挤压后的中点

变化

• 相机与近平面组成的三角形 和 相机与远平面组成的三角形为相似三角形，所以近平面上的点$(x^{\prime },y^{\prime },z^{\prime })$的$y^{\prime }$坐标为$y^{\prime }=\frac{n}{z}y$
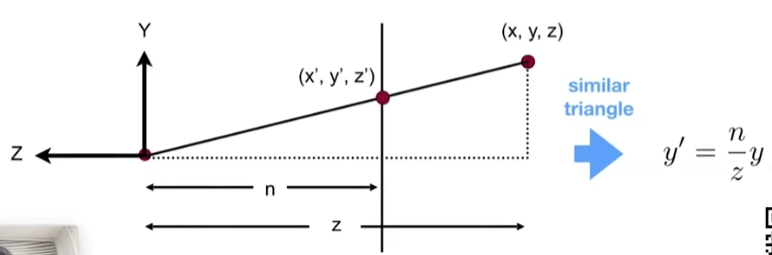
• 通过以上推论，则可以得出$y^{\prime }=\frac{n}{z}y$以及$x^{\prime }=\frac{n}{z}x$，在齐次坐标中的表示则为：

$$M_{persp\to ortho}^{(4\times 4)}\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)\Rightarrow \left(\begin{array}{c}nx/z\\ ny/z\\ unknow\\ 1\end{array}\right)\stackrel{mult.z}{\Rightarrow }\left(\begin{array}{c}nx\\ ny\\ unknow\\ z\end{array}\right)$$

• 则$M_{persp\to ortho}^{(4\times 4)}$ 可解得

$$\left(\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{array}\right)$$

• 此时仍不知道$z$如何运算，只知道近平面与远平面的$z$不会变化，其他$z$值对应的$z^{\prime }$可能变化
• 因为近平面任意点的z并不会变化，所以会有

$$M_{persp\to ortho}^{(4\times 4)}\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}nx\\ ny\\ unknow\\ z\end{array}\right)\stackrel{replacezton}{\Rightarrow }\left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)=\left(\begin{array}{c}nx\\ ny\\ n^2\\ n\end{array}\right)$$

设$M_{persp\to ortho}^{(4\times 4)}$第三行为$\left(\begin{array}{cccc}A& B& C& D\end{array}\right)$前两个数$A,B$必为0，且有$C\times n+D=n^2$ 又因为远平面的中心点

$$M_{persp\to ortho}^{(4\times 4)}\left(\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right)\stackrel{mult.tof}{\Rightarrow }\left(\begin{array}{c}0\\ 0\\ f^2\\ f\end{array}\right)$$

则有$C\times f+D=f^2$ 解方程可得： $C=n+f,D=-nf$ 可得

$$M_{persp\to ortho}^{(4\times 4)}=\left(\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right)$$